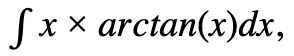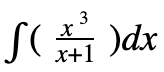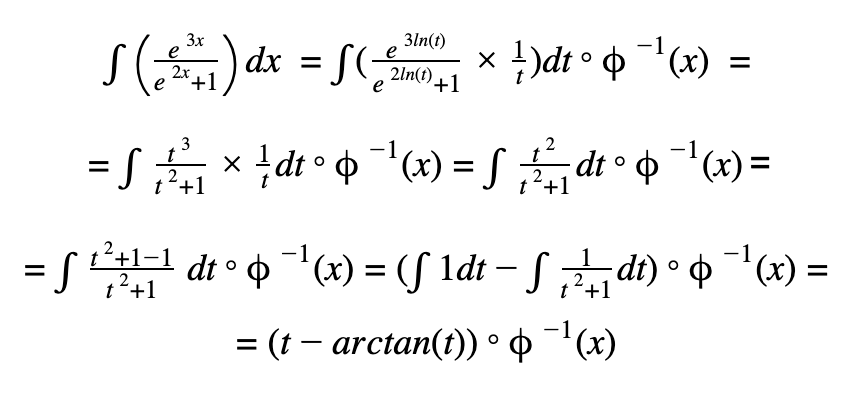Aulas de Primitivas
Neste capítulo vais ter a oportunidade de aprender: primitivas imediatas, primitivação por partes, primitivação por fracções racionais e por substituição, preparado?
O que são primitivas? São as funções inversas das derivadas.
Calcular Primitivas
Como podemos calcular primitivas? Imagina que pretendemos derivar o sen(x), como resultado obtemos o cos(x), logo, se quisermos primitivar o cos(x), o resultado que obtemos é sen(x); ou seja:

.
Para aprenderes a primitivar é muito importante praticares. Neste capítulo vais ter muitos exemplos de primitivas e também um conjunto de exercícios com resoluções feitas por mim para poderes consolidar a matéria.
O primeiro passo para aprenderes a primitivar é memorizares as regras das derivadas, porque a pergunta que vais fazer a ti próprio quando queres primitivar uma função f(x) será:
Qual é a função cuja derivada é f(x) ?
Depois de saberes todas as regras de derivação estás pronto para aprenderes primitivas.
No início do caminho temos as primitivas imediatas, ou seja, aquelas que existe diretamente uma função cuja derivada é f(x).
Na segunda etapa temos primitivas não imediatas, e caso se tratem de produtos usaremos o método de primitivação por partes.
Tal como em qualquer caminho quando o que aprendemos para trás não resolve o problema precisamos de prosseguir.
Se a nossa primitiva é um quociente polinomial utilizamos o método dos quocientes indeterminados para simplificarmos a primitiva.
Finalmente quando tentamos todas as abordagens e não conseguimos resolver a primitiva devemos utilizar o método de primitivação por substituição.
Primitivas Imediatas
Para as primitivas imediatas são dadas regras em que a sua aplicação é directa.
A primitiva ƒ(x) diz-se imediata se existir directamente uma função cuja derivada é ƒ(x).
Tabela de Primitivas
A tabela de primitivas imediatas é dada nas minhas aulas, onde vais encontrar para cada fórmula, vários exercícios de exemplo.

- esta primeira regra utiliza-se sempre que temos uma primitiva de um polinómio, ou um expoente em que a base é apenas x.

- esta regra utiliza-se para qualquer tipo de função desde que esteja a multiplicar pela sua derivada.

- nesta regra o numerador tem de ser 1 e o do denominador x.

- nesta regra o numerador tem de ser a derivada do denominador, e u pode ser uma função qualquer.
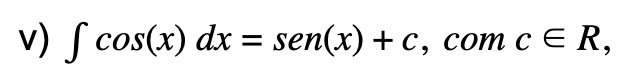
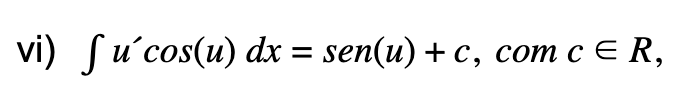
- nesta regra u pode ser uma função qualquer, sendo u´ a sua derivada.


- nesta regra u pode ser uma função qualquer.


- nesta regra u pode ser uma função qualquer.


- nesta regra u pode ser uma função qualquer.


- nesta regra u pode ser uma função qualquer.
Primitivas Imediatas Exercícios Resolvidos
Vou apresentar-te alguns exercícios resolvidos por mim de primitivas imediatas,

esta primitiva é imediata, para a resolvermos basta desenvolvermos o caso notável, repara,


nesta primitiva basta colocarmos dentro da primitiva a constante 2 e temos
 logo a sua primitiva é um logaritmo,
logo a sua primitiva é um logaritmo,


mais uma vez estamos perante uma primitiva imediata, pois temos
u´cos(u), logo a primitiva será sen(u),


neste exercício temos
 logo a primitiva será arcsen(u),
logo a primitiva será arcsen(u),


nesta primitiva primeiro temos de simplifica-la,

nesta fase já é fácil percebermos que estamos perante uma primitiva imediata,

Primitivação por Partes
O método de primitivação por partes aplica-se quando temos uma primitiva que não é imediata e é um produto, a sua fórmula é

onde u representa a primitiva de u ' e v ' a derivada de v . Neste curso primitivo por este método, x.cos(x), x.ex, ln(x), cos2(x), x2.ex entre outras funções.
Primitivação por partes exercícios resolvidos
Vou utilizar o método de primitivação por partes e explicar-te alguns exercícios resolvidos por mim:

esta primitiva não é imediata pois a derivada do argumento do cosseno não está presente, ou seja, não temos u´cos(u).
Como a primitiva não é imediata e é um produto, o método que mais se adequa é primitivação por partes.
O x será o nosso v e cos(3x) será o u´, uma vez que a derivada de x é 1,

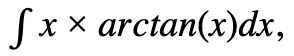
vamos resolver utilizando primitivação por partes.
Onde x será u´ e arctan(x) será o v, uma vez que a função arctan(x) não é uma primitiva imediata, apenas a conseguimos derivar,


neste exercício temos de utilizar primitivação por partes duas vezes.
Quando aplicamos o método pela primeira vez, surge uma primitiva que ainda não é imediata.
A nossa escolha será: x2 o v, pois ao derivarmos baixamos o grau do polinómio, a função ex será o u´ uma vez que a sua primitiva é imediata,

agora voltamos a aplicar o método de primitivação por partes à primitiva

ficando,

Primitivas de Funções Racionais
Estamos perante uma primitiva de funções racionais quando temos um quociente polinomial que não é imediata, por exemplo:

Como resolvemos?
Primeiro vemos de que tipo são os zeros do denominador, e concluímos que temos um zero com multiplicidade 3 e um outro zero simples, então simplificamos a primitiva da seguinte forma,

depois vamos encontrar o valor das constantes A,B,C,D e ficamos com 4 primitivas imediatas. Nos meus vídeos tens este exercícios resolvido passo a passo.
Neste tipo de primitivas fiz esquemas que te vão ajudar a perceber quantos tipos de zeros existem e como se resolvem.
Primitivas de funções racionais exercícios resolvidos
Vou utilizar as primitivas de funções racionais e explicar-te alguns exercícios resolvidos por mim:
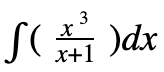
quando olhamos para esta primitiva o nosso primeiro pensamento deve ser questionarmos, será esta primitiva imediata? Não é imediata pois trata-se de um quociente polinomial em que o grau do numerador é superior ao grau do denominador.
Estamos perante a primitiva de uma função racional imprópria, a forma de resolver a primitiva é simplificar o quociente fazendo uma divisão polinomial e desta forma transformar numa função racional própria.

e com esta pequena simplificação passamos a ter 4 primitivas imediatas,


estamos perante uma função racional própria, pois o grau do denominador é superior ao grau do denominador.
Porém não é uma primitiva imediata uma vez que no numerador não temos a derivada do denominador, isto é, não temos

Para resolvermos esta primitiva em primeiro lugar vamos encontrar os zeros do denominador através da fórmula resolvente.

agora vamos utilizar o método dos coeficientes indeterminados para calcular o valor das constantes A e B, depois ficamos com duas primitivas imediatas,

resolvendo este sistema de duas equações obtemos











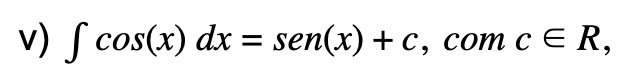
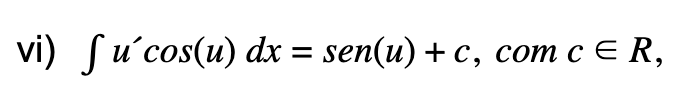











 logo a sua primitiva é um logaritmo,
logo a sua primitiva é um logaritmo,



 logo a primitiva será arcsen(u),
logo a primitiva será arcsen(u),